Triângulo de Pascal
O triângulo ao lado, dividido em linhas e colunas, é composto de números binomiais.
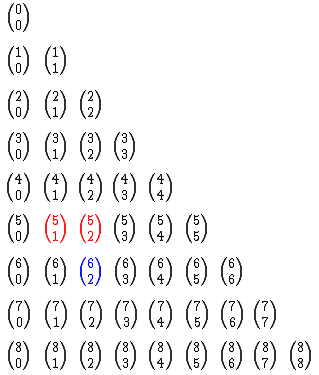
Em cada número binomial 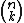 , n, o numerador, está relacionado ao número da linha e k, o denominador, ao número da coluna.
, n, o numerador, está relacionado ao número da linha e k, o denominador, ao número da coluna.
Observe que na quinta linha temos 5 números binomiais, todos eles com numerador igual a 4.
Veja também que na terceira coluna todos os números binomiais possuem 2 como denominador.
Resumindo, o numerador de todos os números binomiais de uma determinada linha é o mesmo, assim como o denominador de todos os números binomiais de uma certa coluna é igual ao número da coluna.
Linhas e colunas começam em 0.
As linhas de um Triângulo de Pascal possuem uma quantidade finita de elementos, que é igual ao número da linha mais 1. Por exemplo, a quinta linha, que é a de número 4, possui 5 elementos.
Já a quantidade de elementos por coluna é infinita, pois o número de linhas do Triângulo de Pascal também é infinito.
Portanto, na figura acima temos apenas um fragmento do Triângulo de Pascal.

Agora vejamos este mesmo fragmento do triângulo já com os números binomiais substituídos por seus respectivos valores:
Repare que todas as linhas começam e terminam com o número 1. Isto já era de se esperar, pois como vimos no estudo dos números binomiais, 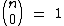 e
e 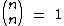 .
.
Construindo um Triângulo de Pascal
Para construirmos um triângulo como este podemos calcular os números binomiais, um a um. Vejamos como exemplo os números destacados em vermelho e em azul:
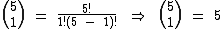
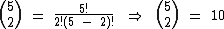
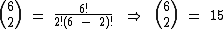
Embora simples, o processo é bastante trabalhoso, principalmente à medida que o número da linha vai crescendo, mas felizmente há uma alternativa mais simples para realizarmos a montagem de um triângulo destes.
Vamos analisar os mesmos três números destacados em vermelho e em azul.
Repare que o número 15 pode ser obtido se somarmos o número que está na linha imediatamente acima ( 10 ) com o vizinho da esquerda deste número ( 5 ).
Veja que este raciocínio serve para todos os números do triângulo, com exceção do primeiro e do último número de cada linha.
Este algoritmo é muito bom quando estamos construindo o triângulo linha a linha, pois sempre conhecemos o conteúdo acima da linha que estamos criando, mas como proceder para obter apenas os números de uma determinada linha, sem conhecermos os números da linha acima?
Como Obter os Números de uma Determinada Linha do Triângulo de Pascal não Conhecendo a Linha Anterior?
Uma solução óbvia é calcularmos cada um dos números binomiais que a formam, mas há um outro algoritmo menos trabalhoso, com o qual evitamos trabalhar com fatoriais e com cálculos de combinação simples.
 Vamos por exemplo obter, um a um, os números da linha 7 sem nos referirmos aos números da linha 6.
Vamos por exemplo obter, um a um, os números da linha 7 sem nos referirmos aos números da linha 6.
Como já vimos, todas as linhas começam com o número 1:
1
A partir da segunda linha o segundo número é igual ao número da própria linha, então o segundo número da linha 7 é 7:
1, 7
Para obtermos o terceiro número vamos multiplicar o segundo, que é 7, por 6/2:
1, 7, 21
O quarto número será o terceiro, que é 21, multiplicado por 5/3, que dá 35:
1, 7, 21, 35
Podemos obter o quinto número multiplicando o quarto por 4/4, mas vamos analisar o que estamos fazendo:
A partir do segundo número começamos multiplicando por 6/2. No caso da primeira fração, o numerador escolhido será sempre uma unidade menor que o número da linha, no caso 7 - 1. Já para o denominador, sempre começamos com o número 2.
A cada número que vamos obtendo acrescentamos uma unidade ao numerador e subtraímos uma unidade do denominador: 6/2, 5/3, 4/4.
Veja que inicialmente o numerador é maior que o denominador. Quando deixa de ser é que já calculamos pelo menos a metade dos números da linha.
Como podemos observar na figura acima, em cada linha do Triângulo de Pascal, os números equidistantes dos extremos são iguais. Então, embora possamos continuar os cálculos multiplicando por 4/4, 3/5, 2/6 e 1/7, é muito mais prático espelharmos os números já obtidos:
1, 7, 21, 35, 35, 21, 7, 1
Estes são os oito números que compõe a linha sete.
 Vamos fazer a mesma coisa para a linha 8:
Vamos fazer a mesma coisa para a linha 8:
1, 8
Multiplicando 8 por 7/2, obtemos 28:
1, 8, 28
Multiplicando 28 por 6/3, obtemos 56:
1, 8, 28, 56
Multiplicando 56 por 5/4, obtemos 70:
1, 8, 28, 56, 70
Agora multiplicaríamos 70 por 4/5, mas como o numerador já não é maior que o denominador, é melhor pararmos os cálculos e realizarmos o espelhamento, só que agora há uma diferença.
No caso da linha 7 chegamos à fração 4/4, com numerador igual ao denominador.
No caso da linha 8 obtivemos à fração 4/5, com numerador menor que o denominador.
Isto ocorre, pois a linha 7 possui uma quantidade par de números, ao passo que linha 8 possui uma quantidade ímpar.
Neste caso não espelhamos o último número obtido, no caso o 70, apenas os demais:
1, 8, 28, 56, 70, 56, 28, 8, 1
Estes são os nove números que compõe a linha oito. Veja que se o número 70 tivesse sido espelhado, teríamos dez números na linha e não nove que é a quantidade correta.
Na tabela abaixo vemos de novo como obter os números da linha 7. Observe que nela começamos os cálculos multiplicando o primeiro, 1, pela fração 7/1, obtendo assim o segundo número:
| |
1 . 7/1 = |
7 . 6/2 = |
21 . 5/3 = |
35 . 4/4 = |
35 . 3/5 = |
21 . 2/6 = |
7 . 1/7 = |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
Nesta outra tabela fazemos o mesmo em relação à linha 8:
| |
1 . 8/1 = |
8 . 7/2 = |
28 . 6/3 = |
56 . 5/4 = |
70 . 4/5 = |
56 . 3/6 = |
28 . 2/7 = |
8 . 1/8 = |
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
Os números que destacamos em laranja são aqueles que não necessariamente precisam ser calculados, pois ou são os dois primeiros da linha, ou são os que podem ser espelhados, conforme explicamos acima.
Se você estiver interessado em verificar o que aprendeu, calcule os números da linha 12.
Apenas para que você possa realizar a conferência, esses números são:
1, 12, 66, 220, 495, 792, 924, 792, 495, 220, 66, 12, 1
Relação de Stifel
Podemos verificar visualmente no Triângulo de Pascal a Relação de Stifel, tratada no estudo sobre os números binomiais:
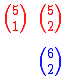
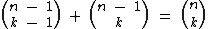
Nos dois triângulos no início desta página temos três números destacados. Dois números em vermelho e um número em azul.
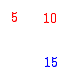
Vimos no começo do artigo que o número 15 pode ser obtido se somarmos o número que está na linha imediatamente acima ( 10 ) com o vizinho da esquerda deste número ( 5 ).
O número 15 está na linha n = 6, coluna k = 2, então substituindo n e k na Relação de Stifel por estes valores, temos:
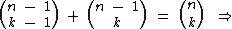
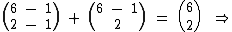
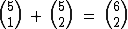
É a Relação de Stifel que nos permite somar os referidos números 5 e 10 e obtermos como resultado o número 15 citado:
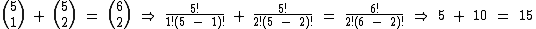
Soma dos Números de uma Linha
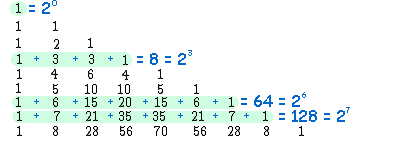
Qualquer que seja a linha de um Triângulo de Pascal, se somarmos os números nela contidos, sempre iremos obter como total uma potência de 2, cujo expoente é o próprio número da linha.
Vejamos alguns exemplos:
 Linha 0:
Linha 0:
1 = 20
 Linha 3:
Linha 3:
1 + 3 + 3 + 1 = 8 = 23
 Linha 6:
Linha 6:
1 + 6 + 15 + 20 + 15 + 6 + 1 = 64 = 26
 Linha 7:
Linha 7:
1 + 7 + 21 + 35 + 35 + 21 + 7 + 1 = 128 = 27
Soma dos Números de uma Coluna até Determinada Linha
Se somarmos os primeiros números de uma coluna qualquer até determinada linha, esta soma será igual ao número na próxima linha e próxima coluna.
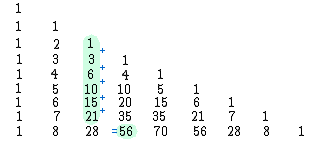
Vamos somar, por exemplo, os 6 primeiros números da coluna 2, isto é, da terceira coluna:
 1 + 3 + 6 + 10 + 15 + 21 = 56
1 + 3 + 6 + 10 + 15 + 21 = 56
Veja que 56 é justamente o número na linha 8, coluna 3, uma coluna após a coluna somada e uma linha abaixo.
Exatamente o valor do número binomial nesta posição: 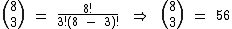
Soma dos Números de uma Diagonal até Determinada Linha
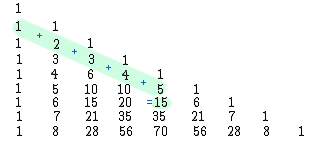
Se somarmos os primeiros números de uma diagonal qualquer até uma certa linha, como fizemos no triângulo ao lado, o total obtido será igual ao número na próxima linha e coluna da última coluna somada:
 1 + 2 + 3 + 4 + 5 = 15
1 + 2 + 3 + 4 + 5 = 15
Note que a partir de qualquer linha, temos que começar a totalização dos números na primeira coluna e a cada número somado avançamos para a próxima coluna e descemos para a próxima linha.
Números de Fibonacci nas Diagonais do Triângulo de Pascal
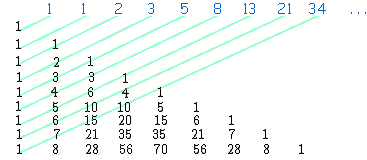
Os números de Fibonacci formam uma sequência numérica infinita, onde a partir do terceiro número, os números são obtidos através da soma dos dois números anteriores.
Os dois primeiros números da sequência de Fibonacci são iguais a 1 e todos os demais números são obtidos a partir da soma dos dois números anteriores, assim temos:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...
Observe no triângulo ao lado que ao somarmos os números nas diagonais conforme mostrado, as somas obtidas vão formando a sequência de sequência de Fibonacci.
