Desmitificando o Cálculo de Probabilidades
Para muitos o cálculo de probabilidades é a personificação do Bicho Papão. Esta página foi escrita justamente para mostrar que na verdade ele não passa de um lindo gatinho de olhos verdes.
Na página sobre conceitos da probabilidade a definimos como sendo a razão do número de elementos de um evento para o número de elementos do espaço amostral.
O espaço amostral é o conjunto de todos os resultados possíveis de ocorrer
No evento do lançamento de um dado, qual é a probabilidade de cair o número 5?
Nós sabemos que um dado é um cubo que possui as suas faces numeradas de 1 a 6. Em termos de probabilidades o seu espaço amostral é:
S = { 1, 2, 3, 4, 5, 6 }
Como um dado possui seis faces distintas, possuindo apenas uma face igual a 5, a probabilidade de dar este valor é de uma em seis, que podemos representá-la assim:
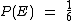
Note que não há segredo, como dito acima, a probabilidade de um evento ocorrer nada mais é que a razão do seu número de elementos para o número de elementos do espaço amostral.
Obviamente esta é a situação mais simples, mas no fundo todas as situações irão se resumir a isto. Para que a explicação fique mais simples e também mais fácil o entendimento, vamos continuar trabalhando em cima de exemplos.
Exemplos
Um jovem casal pretende ter 3 filhos. Qual é a probabilidade de que tenham pelo menos uma menina?
Quantas são as combinações possíveis, ou em outras palavras, qual é o número de elementos do espaço amostral?
Para cada filho temos duas possibilidades, ou é masculino ou é feminino, então pelo princípio fundamental da contagem temos que 2 . 2 . 2 = 8, portanto há 8 agrupamentos possíveis.
Dos 8 agrupamentos possíveis um deles é formado apenas por meninos, todos os outros 7 possuem ao menos uma menina, portanto a probabilidade de que o casal tenha pelo menos uma menina é a razão de 7 para 8:
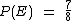
Se representarmos por M os filhos do sexo masculino e por F os filhos do sexo feminino, podemos representar assim o espaço amostral:
S = { (F, F, F), (F, F, M), (F, M, F), (F, M, M), (M, F, F), (M, F, M), (M, M, F), (M, M, M) }
Confirmando o que foi dito acima, apenas o último elemento não possui meninas, então 7 dos 8 eventos possíveis satisfazem à condição do enunciado, confirmando também a probabilidade calculada acima.
A probabilidade de que tenham pelo menos uma menina é 7/8.
Qual é a probabilidade do jovem casal vir a ter tanto meninos quanto meninas?
Analisando o espaço amostral deduzimos que o evento E = { (F, F, M), (F, M, F), (F, M, M), (M, F, F), (M, F, M), (M, M, F) } satisfaz as condições do enunciado, pois seus elementos possuem tanto meninos quanto meninas. Como este evento possui 6 elementos, que representamos por n(E) = 6, então a probabilidade será:
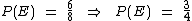
A probabilidade de venham a ter tanto meninos quanto meninas é 3/4.
Qual é a probabilidade de que venham a ter mais meninas que meninos?
A partir do espaço amostral vemos que o evento E = { (F, F, F), (F, F, M), (F, M, F), (M, F, F) } satisfaz a condição desejada. Visto que este evento possui 4 elementos, temos que a probabilidade será:
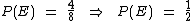
Já que estamos levando em consideração apenas a existência de dois sexos, sem levarmos em conta fatores biológicos, por exemplo, este resultado já era de se esperar, pois obviamente a probabilidade de que venham a ter mais meninos que meninas deve ser a mesma, pois 1/2 + 1/2 = 1. Este 1 representa o número de elementos do espaço amostral e como a soma deve ser igual a 1, obviamente as duas probabilidades iguais devem ser iguais a 1/2.
Em outra página é explicado como solucionar problemas deste tipo através do termo geral do Binômio de Newton.
A probabilidade de venham a ter mais meninas que meninos é 1/2.
No lançamento de um dados qual é a probabilidade de obtermos um 3 ou um 5?
No início deste tópico vimos que a probabilidade de ocorrer um 5 no lançamento de um dado é 1/6. Assim como acontece com o 5, também só há um 3 no dado, então a probabilidade de ocorrer um 3 também é 1/6. Como a ocorrência de um 3 inibe a ocorrência de um 5 e vice-versa, pois em um único lançamento se acontecer um, não pode acontecer o outro, dizemos que eles são eventos mutuamente exclusivos.
Quando utilizamos a conjunção "OU", neste exemplo desejamos obter 3 ou 5, estamos tratando da união de probabilidades. Quando, assim como neste exemplo, os eventos são mutuamente exclusivos, devemos somar as probabilidades individuais. Então temos que 1/6 + 1/6 = 1/3, que é a probabilidade procurada.
Se os eventos não fossem mutuamente exclusivos, a soma ainda valeria, mas precisaríamos subtrair deste total a probabilidade da ocorrência dos elementos na intersecção destes eventos. Isto é estudado em maiores detalhes na página sobre união de dois eventos.
A probabilidade de obtermos um 3 ou um 5 é 1/3.
Em lançamentos sucessivos de um dado qual é a probabilidade de obtermos um 3 e depois um 5?
Repare que agora estamos utilizando a conjunção "E". Quando temos a ocorrência de vários eventos independentes e sucessivos, estamos tratando do produto de probabilidades. A probabilidade de que os eventos ocorram nesta ordem é obtida através do produto das probabilidades individuais.
Neste exemplo temos que 1/6 . 1/6 = 1/36.
A probabilidade de obtermos um 3 e depois um 5 é 1/36.
Pronto, agora você já tem uma melhor ideia de como são realizados os cálculos de probabilidades. Você viu que o assunto não é nenhum bicho papão, mas não se descuide com o lindo gatinho de olhos verdes, pois ele poderá surpreendê-lo. O cálculo de probabilidades necessita que o enunciado seja lido com bastante atenção, para que não tenhamos uma compreensão errônea do problema.
Nas demais páginas sobre este tema você terá maiores detalhes sobre a matéria.
