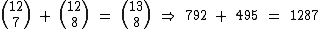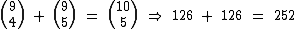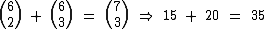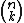é a representação do número binomial de numerador n e denominador k, ou então do número binomial n sobre k.

Sendo n ≥ k, com n e k pertencentes ao conjunto do números naturais, o número binomial 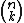é dado por:

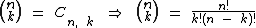
Note que os números binomiais, ou coeficientes binomiais, são obtidos através da combinações simples de n elementos distintos, agrupados k a k, com k ≤ n.

Realizando a simplificação de fatoriais chegamos a esta outra expressão:

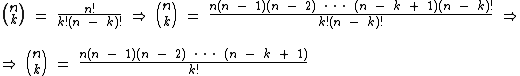
Alguns números binomiais podem ser obtidos sem precisarmos realizar o cálculo da combinação simples, por exemplo:

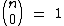, pois: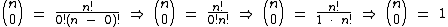

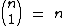, pois: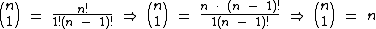

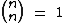, pois: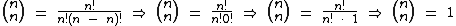

Igualdade de Números Binomiais

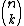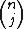Dois números binomiais e , com 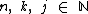, são iguais se:

• k = j, ou
•  
• k + j = n
•  

Segundo a propriedade dos termos complementares, se fizermos j = n - k, temos ainda que:

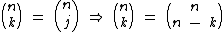
Em outras palavras, para que dois números binomiais 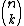e 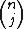sejam iguais, k e j devem ser iguais ou complementares.

Exemplos de Igualdade entre Números Binomiais

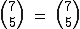
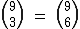
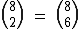
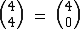
Relação de Stifel

A Relação de Stifel ou Regra de Pascal, nos permite realizar a seguinte igualdade:

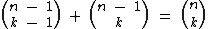
Esta regra é válida para: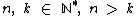

Exemplos Utilizando a Relação de Stifel