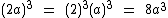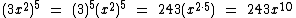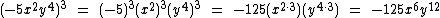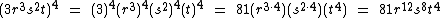Anteriormente tivemos um introdução ao cálculo algébrico, onde fizemos a resolução de um problema usando tanto o método aritmético, quanto o método algébrico. Ocasião na qual fomos bastante superficiais. Agora vamos nos aprofundar mais um pouco tratando os Monômios.

Vimos que no cálculo algébrico utilizamos letras para representar valores que desconhecemos, e as chamamos de variável ou incógnita.

Definição de Monômio

Denominamos monômio ou termo algébrico quaisquer expressões algébricas representadas por um número, por uma incógnita, ou pelo produto de números e incógnitas, assim 2, x, 2x e -3xy² são exemplos de termos algébricos ou monômios.

Identificando as Partes de um Monômio

No monômio -3xy² o número -3 representa o seu coeficiente numérico e a sua parte literal é representada por xy².

Por convenção omitimos o coeficiente numérico quando ele é igual a 1, escrevemos x em vez de escrevermos 1x, por exemplo, ou então -x no lugar de -1x.

Temos um monômio nulo quando o coeficiente numérico é igual a 0, assim o termo algébrico 0x² é igual a 0.

Acima utilizamos o número 2 como um exemplo de monômio. De fato todo número real é um monômio, só que sem a parte literal.

Grau de um Monômio

O grau de um monômio é obtido através da soma dos expoentes de todas as variáveis. O coeficiente numérico deve ser diferente de zero, caso contrário o monômio será nulo.

7xy² é um monômio de grau 3, já que o expoente de x subentende-se que seja igual a 1 e o de y é igual a 2.

O monômio -5x⁴ é de grau 4, pois só possui a variável x com expoente igual a 4.

18² é de grau 0, pois é um monômio sem a parte literal.

Grau de um Monômio em Relação a uma Certa Incógnita

Embora o monômio 7xy² seja de grau 3 se o considerarmos como um todo, analisando-o apenas em relação à variável x, ele será de grau 1, mas se o analisarmos em relação à incógnita y ele será de grau 2, isto porque o grau do monômio corresponderá ao expoente da variável em questão.

Monômios Semelhantes

Observe os três termos algébricos abaixo:

-5x⁴y

2x⁴y

7xy²

Note que os dois primeiros possuem a mesma parte literal, já o terceiro embora partilhe das mesmas variáveis, possui uma parte literal distinta, pois os expoentes das respectivas variáveis são diferentes.

Redução de Termos Semelhantes

Por possuírem a mesma parte literal os dois primeiros termos algébricos são denominados monômios semelhantes. Este conceito é muito importante, pois podemos reduzir uma expressão algébrica, contendo vários termos semelhantes, através da soma algébrica destes termos.

Adição de Monômios

Se você tiver 3 bananas e 2 maçãs, ao ganhar mais 2 bananas e 2 maçãs, você ficará com 5 bananas e 4 maçãs. Note que somamos bananas com bananas e maçãs com maçãs. O mesmo raciocínio é aplicado à soma algébrica de monômios em relação aos termos semelhantes.

Observe a seguinte expressão formada pela soma algébrica de três monômios semelhantes:

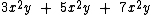
Como os três termos algébricos são semelhantes podemos reduzi-los a um único monômio somando os coeficientes numéricos e mantendo a parte literal:

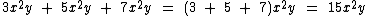
Veja outros exemplos:

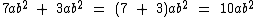
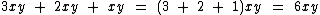
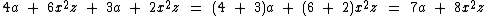
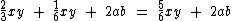
Você deve ter percebido que no quarto exemplo somamos os dois primeiros termos, mas não o último, pois este não é semelhante a eles.

Subtração de Monômios

Em sendo a subtração a operação inversa da adição, o que explicamos acima para a soma, vale também de forma análoga para a diferença de monômios.

Vejamos alguns exemplos:

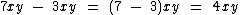
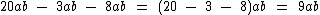
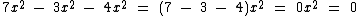
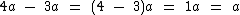
Multiplicação de Monômios

A multiplicação de monômios é realizada simplesmente se multiplicando os coeficientes numéricos entre si, assim como a parte literal.

Veja o seguinte exemplo:

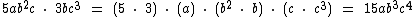
Sabemos que na multiplicação de potências de mesma base mantemos a base e somamos os expoentes. Se você observar, verá que além da multiplicação dos coeficientes numéricos, foi exatamente isto o que fizemos no produto acima.

A variável a tem expoente 1 no primeiro termo algébrico e não ocorre no segundo termo. Portanto mantém-se com o expoente igual a 1.

A incógnita b tem os expoentes 2 e 1 no primeiro e segundo termo respectivamente, totalizando 3 no expoente.

Já a variável c tem os expoentes 1 e 3, que somados totalizam um expoente igual a 4.

Então como regra geral para multiplicarmos monômios é multiplicarmos os coeficientes e para cada variável somarmos os seus expoentes.

Vejamos outros exemplos:

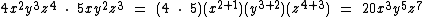
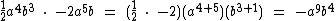
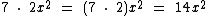
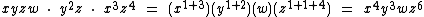
Divisão de Monômios

Agora vamos tratar a operação inversa da multiplicação, a divisão de monômios.

Os procedimentos serão semelhantes ao do caso anterior, iremos dividir os coeficientes numéricos e subtrair os expoentes das incógnitas da parte literal.

Observe este exemplo:

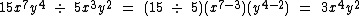
O exemplo é autoexplicativo, mas para que não fique qualquer dúvida, vamos comentá-lo.

O coeficiente numérico foi obtido pela divisão dos dois coeficientes originais.

A variável x possui respectivamente os expoentes 7 e 3, então subtraindo o segundo do primeiro obtemos o expoente 4.

Por fim a incógnita y que tem expoente 4 no primeiro monômio e 2 no segundo, fica com o expoente 2, resultante de 4 - 2.

Veja mais estes outros exemplos:

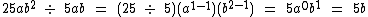
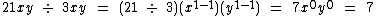
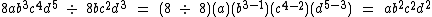
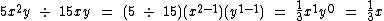
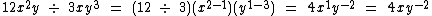
Repare que no último exemplo a variável y terminou com um expoente negativo. Conforme estudado no tópico sobre potenciação, podemos escrever esta expressão na forma de uma fração:

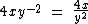
Exponenciação de Monômios

Já vimos que a potência do produto de dois ou mais fatores é igual ao produto de cada um destes fatores elevados ao referido expoente, na potenciação de monômios aplicamos o mesmo princípio.

Vejamos este exemplo:

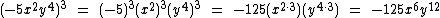
Note que transformamos a potência de produtos, nos produtos de potências. Assim elevamos o coeficiente numérico e cada uma das potências das variáveis ao expoente 3.

-5³ resulta em -125.

(x²)³ como sabemos é igual a x^2 . 3 que é igual a x⁶.

Assim como (y⁴)³ sabemos que é igual a y^4 . 3 que é igual a y¹².

E para terminar este tópico vamos a mais alguns exemplos: