Critérios de Divisibilidade
Introdução
Se você procurar pela Internet, irá encontrar dezenas de sites que falam sobre este assunto, alguns muito bons por sinal, mas a grande maioria deles embora apresentem critérios de divisibilidade para uma vasta uma gama de divisores, não menciona nada que possa explicar o por que de tais critérios, não explicam nada sobre em que eles se baseiam.
O intuito desta página é mostrar os critérios de divisibilidade dos números naturais, que possuem alguma utilidade prática, visto que em muitos critérios é mais rápido e fácil se realizar a divisão, do que se aplicar tais critérios e também mostrar de forma simples, em que se baseiam tais critérios.
Para isto antes de chegarmos aos critérios, você precisa entender alguns conceitos.
Compreendendo o Conceito de Divisibilidade
Na página Múltiplos de um Número Natural foi dito que "o número 15 é múltiplo de 3 porque 15 é divisível por 3". A recíproca também é verdadeira, isto é, 15 é divisível por 3 porque 15 é múltiplo de 3, mas o que exatamente significa "15 é múltiplo de 3"?
Significa que se irmos somando o número 3 várias vezes, acabaremos chegando em 15, precisamente temos que 3 + 3 + 3 + 3 + 3 = 15
Este é o princípio base da multiplicação e também da divisibilidade, pois um número a só é divisível por um número b, quando este número a for formado por n vezes o número b. Note que estamos trabalhando no universo dos números naturais.
Para que fique mais claro, veja a figura abaixo:
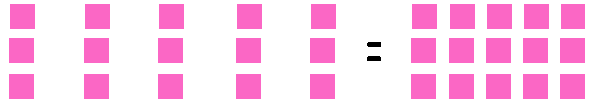
Podemos dizer que 15 é divisível por 3 porque o número 3 está contido exatamente cinco vezes no número 15 sem deixar resto.
Se retirarmos quantos 3 for possível retirarmos não restará nada, ou seja, o resto será zero.
Agora veja a figura abaixo como seria a situação do número 4 ainda em relação ao divisor 3:
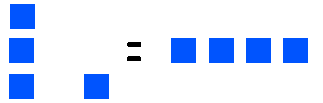
Podemos facilmente observar que o número 3 está contido uma única vez no número 4, mas desta vez há uma pequena sobra, há um resto de 1, ou seja, 4 não é divisível por 3 porque tal divisão não é exata pois apresenta um resto de 1.
Se retirarmos quantos 3 for possível retirarmos, ainda continuaremos com resto de um.
Aqui vale lembrar que o resto de uma divisão sempre será menor que o divisor. O resto de uma divisão por três sempre será menor que três. Se você realizar uma divisão qualquer e o resto for maior ou igual ao divisor, não tenha a menor sombra de dúvida de que a divisão está errada.
Continuando vamos ver agora a situação do número 5 também ainda em relação ao divisor 3:
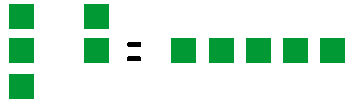
Tal como no caso anterior, 5 não é divisível por 3, porque há um resto de 2.
Se retirarmos quantos 3 for possível retirarmos, ainda continuaremos com um resto de dois.
E se somarmos os dois números, como ficaria a divisibilidade por três?
Vamos ver mais uma figura:

Neste caso vemos que 4 + 5 é divisível por 3, pois como podemos ver há três bloquinhos de três sem deixar resto. Então 9 é divisível por 3.
Veja que como no caso do número 15, se retirarmos quantos 3 for possível retirarmos, também não restará nada, o resto também será zero.
Agora com relação aos três blocos de três à esquerda do sinal de igualdade, dê uma maior atenção ao bloco central. Repare que ele é composto por uma parte referente ao número 4 e mais duas partes referentes ao número 5.
Um resto 1 e um resto 2 sozinhos não são divisíveis por três, mas somados são.
A lógica por trás dos critérios de divisibilidade visa eliminar do número que estamos testando, quantas vezes pudermos tirar o divisor em questão, ou algo próximo disto, o que for mais viável. Se não sobrar nada ou se o resto for divisível pelo divisor, é porque o número testado é divisível pelo divisor em questão.
Este é o ponto chave onde se baseia a maioria dos critérios de divisibilidade, afinal de contas a divisão nada mais é que a retirada múltiplas vezes de um número de outro, até que não seja mais possível retirá-lo por insuficiência.
Divisibilidade por 2
Pensando em termos do que foi dito acima, se tivermos um número par qualquer e retirarmos dele quantos 2 for possível retirarmos, o resto será sempre zero, logo todo número par é divisível por dois.
O mesmo não acontece com os números ímpares, pois neste caso o resto sempre será igual a 1.
Mais abaixo no critério de divisibilidade por cinco, você encontra mais explicações sobre o critério de divisibilidade por dois.
Divisibilidade por 3
Agora a experiência começa a ficar interessante.
O número 5478 é divisível por 3?
Quando a soma dos dígitos de um número for divisível por 3, diz-se que este número também será divisível por três, mas qual é a mágica?
Vamos pensar em termos de quantos 3 podemos retirar de 5478.
Sabemos que 5478 também pode ser expresso como 5000 + 400 + 70 + 8.
Quantos 3 podemos retirar de 5000?
Esta é fácil! Sabemos que 3 . 3, 3 . 33, 3 . 333, assim como qualquer outro número natural multiplicado por três, são divisíveis por três, isto quer dizer que podemos eliminá-los que o número resultante ainda continuará divisível ou não, da mesma forma que o número original era antes da subtração.
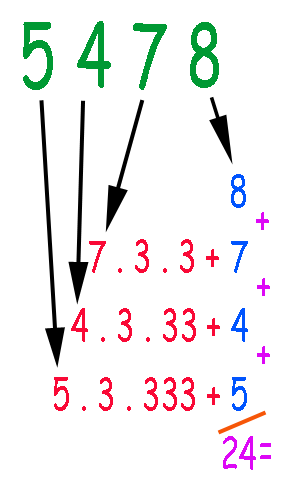
Com isto em mente podemos expressar 5000 como 5 . 3 . 333 + 5, além de 400 como 4 . 3 . 33 + 4 e 70 como 7 . 3 . 3 + 7 tal qual a figura ao lado.
Podemos então dizer que 5478 é igual a:
5 . 3 . 333 + 5 + 4 . 3 . 33 + 4 + 7 . 3 . 3 + 7 + 8
Percebeu a mágica? Ainda não?
Eliminando os termos que estão sendo multiplicados por três, por serem múltiplos dele, resumiremos a expressão a 5 + 4 + 7 + 8.
E então, agora percebeu?
Através deste artifício eliminamos a maioria dos três que pudemos eliminar e as quantidade não trabalhadas correspondem exatamente aos dígitos do número em questão, 5, 4, 7 e 8 que somados totalizam 24, traçado em roxo na figura.
Agora não tem mais segredo, como 24 é divisível por três, então 5478 também é. Se 24 não fosse divisível por três, 5478 também não seria.
Estas operações transformaram o número 5478 no número 24, mas é importante frisar que tudo foi realizado de modo que o número resultante continuasse tendo o mesmo resto que o número original, quando divido por três. Nem é preciso dizer que isto é fundamental, pois quando dividimos o número final por três, devemos obter o mesmo resto que obteríamos ao realizarmos a divisão do número original por três.
Divisibilidade por 4
Consta que quando os dois últimos dígitos de um número formarem um número divisível por 4, o número todo também será.
A razão disto é muito simples. Vamos tomar como exemplo o número 3456. Vamos expressá-lo separando os dois últimos dígitos desta forma: 34 . 100 + 56
Como 100 é múltiplo de 4, então podemos reescrever a expressão assim: 34 . 4 . 25 + 56
Vamos analisar as duas parcelas desta soma.
Como a primeira parcela é divisível por quatro, porque ela é resultado de uma multiplicação por este número, basta que a última parcela (os dois últimos dígitos) também seja divisível por quatro para que a soma, ou o número todo o seja.
Se o número formado pelos dois últimos dígitos não for divisível por quatro, o resto da divisão deles por quatro, também será o mesmo que o resto da divisão do número completo. Por exemplo, o resto da divisão de 123 por 4, é igual ao resto da divisão de 23 por quatro, ou seja, os dois restos são iguais a 3.
Entendeu completamente o que foi explicado neste critério de divisibilidade por 4?
Se entendeu, você pode verificar de forma análoga que o mesmo vale para o número 25, por exemplo. Sabe explicar por quê?
Vai uma pista: A primeira parcela também é resultado de uma multiplicação por 25.
Divisibilidade por 5
Um número é divisível por 5 quando termina em 0 ou 5, pois todo múltiplo de cinco termina ou em zero, ou em cinco.
O raciocínio utilizado para a determinação do critério de divisibilidade por quatro, também pode ser utilizado para de forma análoga provarmos a veracidade dos critérios de divisibilidade por vários outros números. Podemos utilizá-lo em relação à divisibilidade por 2, 4, 5, 8 e muitos outros. Vamos analisar agora o caso do número 5.
Como é mais fácil o entendimento através de exemplos, vamos lá, tomemos como exemplo o número 725. Vamos expressá-lo de forma a isolar o último dígito: 72 . 10 + 5.
Como 10 é múltiplo de 5, a expressão pode ser reescrita como: 72 . 5 . 2 + 5.
Analisando as duas parcelas desta soma como feito no caso do número quatro, temos que a primeira parcela sempre será múltipla de cinco, porque ela é resultado de uma multiplicação por cinco. Para que o número todo seja então divisível por cinco, o único requisito é que a última parcela seja divisível por cinco, o que ocorrerá apenas se ele for igual a zero, ou igual a cinco.
Como a primeira parcela também é resultado de uma multiplicação por dois, se a segunda parcela for par, o número todo será divisível por dois. Esta é uma outra forma de se provar o critério de divisibilidade por dois.
Divisibilidade por 6
Um número é divisível por seis, quando o é também por dois e por três.
A razão disto é muito simples. Já que 6 é o resultado da multiplicação de 2 por 3, qualquer número que seja múltiplo de dois e de três simultaneamente também será de seis.
Isto pode ser verificado facilmente analisando-se as tabuadas de multiplicação do seis e do três. Você pode observar que a tabuada do seis é um apanhado da tabuada do três, onde se selecionou apenas os resultados pares, ou seja, os que também estão nos resultados da tabuada de multiplicação do dois, isto é, além de divisíveis por três, também são divisíveis por dois.
Divisibilidade por 8
Quando os três últimos dígitos de um número formarem um número divisível por 8, o número todo também será divisível por oito.
Como fizemos no caso do número quatro, podemos expressar 5184, por exemplo, como 5 . 1000 + 184.
Mil é divisível por oito, pois como sabemos 8 . 125 é igual a mil. Como a primeira parcela sempre é divisível por oito, quando a última também for o número todo igualmente será.
Divisibilidade por 9
O raciocínio em volta da divisibilidade por 9 é bastante semelhante ao da divisibilidade por 3.
Vamos pensar em termos de quantos 9 podemos retirar de 4635 para desenvolvermos o raciocínio.
Sabemos que 4635 também pode ser expresso como 4000 + 600 + 30 + 5.
Já é claro para nós que 9, 9 . 11, 9 . 111, assim como qualquer outro número natural multiplicado por nove, são divisíveis por nove.
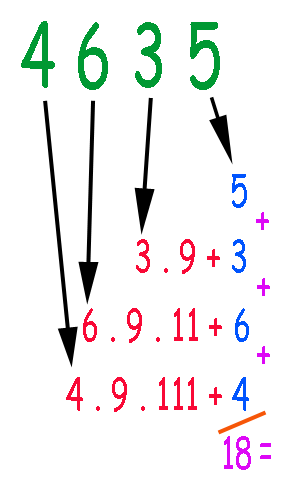
Sabendo disto, como visto na figura ao lado, podemos expressar 4635 como:
4 . 9 . 111 + 4 + 6 . 9 . 11 + 6 + 3 . 9 + 3 + 5
Podemos então eliminar as parcelas que estão sendo multiplicadas por nove, já que isto implicará em um novo número cuja divisão por nove terá como resto o mesmo valor que a divisão de 4635 por nove.
Ficamos então com 4 + 6 + 3 + 5.
Observe que assim como no caso do número três, neste caso também ficamos apenas com os dígitos que compõe o número original, exatamente como queríamos provar.
Totalizando 4 + 6 + 3 + 5 obtemos 18, que como sabemos é divisível por nove.
Divisibilidade por 10
Todo número que termina em zero é divisível por 10.
Isto advém do fato de que todo número nesta condição pode ser expresso como uma multiplicação por dez, por exemplo, 3870 pode ser expresso como 3870 . 10 e em sendo um múltiplo de dez, obviamente é divisível por ele.
Divisibilidade por 11
O critério de divisibilidade por onze dita que um número é divisível por 11 quando a diferença entre a soma dos dígitos de ordem par e os dígitos de ordem ímpar resultar em um múltiplo de 11.
Tomando o número 756789 como exemplo, temos que os dígitos de ordem par são 5, 7 e 9, cuja soma é 21, já os dígitos de ordem ímpar são 7, 6 e 8, que também totalizam 21. A diferença 21 - 21 é igual a 0 que é um múltiplo de 11, por isto 756789 também é um múltiplo de 11.
Assim como no caso dos números três e nove, o critério de divisibilidade por onze segue um raciocínio bem semelhante, como nestes dois casos anteriores.
Pelo próprio critério de divisibilidade por onze, podemos afirmar que 11, 1001, 100001 e assim por diante são divisíveis por onze. Repare que o número de zeros é sempre par, de sorte que o último dígito um sempre seja de ordem par, que subtraído do primeiro dígito um que é de ordem ímpar, sempre resulte em zero, que é divisível por onze.
Acredito que nem seja preciso explicar que números como 99, 9999 e 999999, que são compostos por um número par de dígitos nove, são sempre divisíveis por onze.
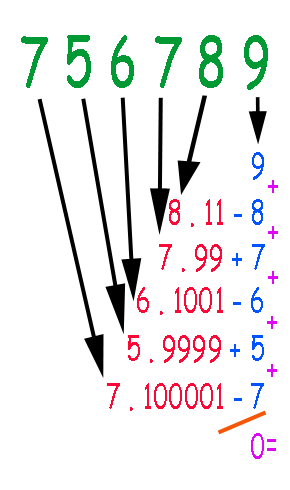
Ainda tomando o número 756789 como exemplo, podemos expressá-lo como 700000 + 50000 + 6000 + 700 + 80 + 9.
O 700000 pode então ser expresso como 7 . 100001 - 7 e 50000 como 5 . 9999 + 5, repare que no primeiro caso estamos subtraindo sete e no segundo estamos adicionando 5 é justamente este artifício que embute o segredo da subtração entre a soma dos dígitos de ordem par e a soma dos de ordem ímpar.
Se você entendeu tudo direitinho até agora, mesmo sem acompanhar pela figura ao lado, já deve ter previsto que para o 6000 iremos utilizar 6 . 1001 - 6, para o 700 utilizaremos 7 . 99 + 7 e para o 80 teremos 8 . 11 - 8. O 9 ficará como nove mesmo.
Então o número 756789 será expresso como:
7 . 100001 - 7 + 5 . 9999 + 5 + 6 . 1001 - 6 + 7 . 99 + 7 + 8 . 11 - 8 + 9
Eliminando as parcelas que estão sendo multiplicadas por um múltiplo de onze, obteremos a seguinte expressão:
-7 + 5 - 6 + 7 - 8 + 9 (veja os números em azul na figura), que totalizada resultará em 0.
Reparou que esta expressão é uma forma de dizer que estamos obtendo a diferença entre a soma dos dígitos de ordem par e a soma dos dígitos de ordem ímpar?
Este processo todo transformou o número 756789 em um outro número, o número 0, mas o fez de sorte que o resto da divisão de qualquer um deles por onze seja o mesmo, que obviamente é zero.
Divisibilidade por 12, 15, 18
No caso da divisibilidade por 6, vimos que isto ocorre quando o número é ao mesmo tempo divisível por 2 e por 3, que são fatores que multiplicados resultam em 6.
Da mesma forma podemos afirmar que um número é divisível por 12, quando também é divisível por 3 e por 4, por 15, quando também é divisível por 3 e por 5 ou que é divisível por 18, quando também é divisível por 2 e por 9.
Divisibilidade por 16
Quando os quatro últimos dígitos de um número formarem um número divisível por 16, o número todo também será divisível por dezesseis.
Como fizemos nos casos dos números quatro e oito, podemos expressar 58336, por exemplo, como 5 . 10000 + 8336.
Como 16 . 625 é igual a dez mil, obviamente dez mil é divisível por 16. Como a primeira parcela é divisível por dezesseis, quando a última também for o número todo igualmente será divisível por dezesseis.
Vamos analisar agora o número 58336 em relação aos critérios de divisibilidade por 2, 4, 8 e 16:
Divisibilidade por 2: 5833 . 10 + 6
Divisibilidade por 4: 583 . 100 + 36
Divisibilidade por 8: 58 . 1000 + 336
Divisibilidade por 16: 5 . 10000 + 8336
Como 2, 4, 8 e 16 são potências de 2 e como 10n = 2n . 5n vamos então analisar desta forma:
Divisibilidade por 2 ( 21 ): 5833 . 21 . 51 + 6 - O número formado pelo último dígito é divisível por 2;
Divisibilidade por 4 ( 22 ): 583 . 22 . 52 + 36 - O número formado pelos 2 últimos dígitos é divisível por 4;
Divisibilidade por 8 ( 23 ): 58 . 23 . 53 + 336 - O número formado pelos 3 últimos dígitos é divisível por 8;
Divisibilidade por 16 ( 24 ): 5 . 24 . 54 + 8336 - O número formado pelos 4 últimos dígitos é divisível por 16.
Repare que a primeira parcela é sempre divisível pelo critério de divisibilidade, pois ela é múltipla de 2n, então se a segunda parcela também for divisível, o número todo também será.
Então temos que um número é divisível por uma potência de dois elevado a n ( 2n ) quando os n últimos dígitos formarem um número divisível por esta potência.
Divisibilidade por 25
Um número é divisível por 25 quando os 2 últimos dígitos formam um número divisível por 25, ou seja, quando termina em 00, 25, 50 ou 75.
Quando falamos sobre a divisibilidade por quatro já foi dada uma pista sobre a divisibilidade por 25, mas vamos a um exemplo para a eliminação de qualquer dúvida.
Tomemos o número 1725 e o expressemos desta forma: 17 . 100 + 25, como cem é múltiplo de 25, vamos então expressar o número assim: 17 . 4 . 25 + 25.
Como você já sabe, já que a primeira parcela é divisível por vinte e cinco, o número todo também o será quando a segunda parcela também o for.
Fica aqui um exercício para você. Assim como no caso das potências de dois, prove que também para as potências de cinco, um número é divisível por uma potência de cinco elevado a n ( 5n ) quando os n últimos dígitos formarem um número divisível por esta potência.
