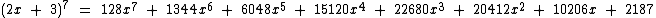Binômio de Newton
Se lhe solicitarmos o resultado de (2x + 3)2 muito provavelmente você o obterá recorrendo aos produtos notáveis, mas e se quiséssemos o resultado de (2x + 3)7, como você procederia?
O método do Binômio de Newton nos permite calcular a enésima potência de um binômio. Este é um bom método a ser utilizado no desenvolvimento de (2x + 3)7.
Fórmula Geral do Desenvolvimento do Binômio de Newton
Segundo o método de Isaac Newton o desenvolvimento de (a + b)n com 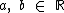 e
e 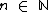 é dado por:
é dado por:
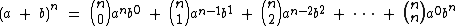
Veja que temos um polinômio com n + 1 termos, onde o coeficiente numérico de cada termo algébrico é dado por um número binomial.
O numerador destes números binomiais é sempre n, já o denominador varia de 0 no primeiro termo, a n no n-ésimo termo.
Observe no polinômio que o expoente de a decresce de n a 0 e de maneira oposta, o expoente de b cresce de 0 a n.
Podemos notar também que a soma dos expoentes de a e b em cada termo é igual n.
Se você acessou o nosso artigo sobre números binomiais, deve saber que o seu desenvolvimento é realizado através da fórmula da combinação simples que aprendemos no estudo da análise combinatória.
Desenvolvendo o Cálculo de (2x + 3)7
Segundo a fórmula geral que vimos acima, o desenvolvimento de (2x + 3)7 será:
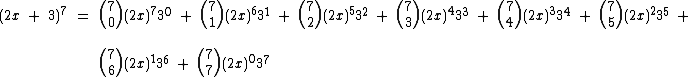
Estas potências não temos dificuldades em resolver, o mais trabalhoso é o cálculo dos coeficientes binomiais, mas felizmente em vez de calculá-los, podemos utilizar a mesma técnica utilizada quando mostramos como obter os números de uma determinada linha do triângulo de pascal não conhecendo a linha anterior, mesmo assim é desejável que você aprenda como são calculados os números binomiais caso você não saiba como fazê-lo.
Na tabela abaixo vemos como obter os números da linha 7 do Triângulo de Pascal, que é a linha que contém todos os números binomiais da expressão acima. Veja que o número da linha é o expoente de (2x + 3)7, ou seja, é igual a n.
A segunda linha desta tabela contém o valor de cada um dos números binomiais da expressão acima.
| |
1 . 7/1 = |
7 . 6/2 = |
21 . 5/3 = |
35 . 4/4 = |
35 . 3/5 = |
21 . 2/6 = |
7 . 1/7 = |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
A tabela é formada coluna por coluna, da esquerda para a direita. O coeficiente binomial da primeira coluna é sempre igual a 1:
Os demais coeficientes são obtidos multiplicando por uma fração o coeficiente anteriormente calculado. As frações seguem a seguinte regra de uma fração para a próxima: O numerador começa em n (7 em nosso exemplo) e decresce até 1. O denominador inicia em 1 e ascende até n.
Então para o segundo coeficiente temos a multiplicação de 1, que é o coeficiente anterior, por 7/1:
Na verdade o segundo coeficiente sempre será igual a n, 7 no caso deste exemplo.
O terceiro coeficiente é obtido multiplicando 7 por 6/2. Veja que subtraímos uma unidade do numerador da fração anterior e adicionamos uma unidade ao seu denominador:
O quarto coeficiente calculamos multiplicando 21 por 5/3:
| |
1 . 7/1 = |
7 . 6/2 = |
21 . 5/3 = |
| 1 | 7 | 21 | 35 |
Continuando este raciocínio obtemos todos os coeficientes:
| |
1 . 7/1 = |
7 . 6/2 = |
21 . 5/3 = |
35 . 4/4 = |
35 . 3/5 = |
21 . 2/6 = |
7 . 1/7 = |
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
Muito provavelmente você esteja intrigado com os números que destacamos em laranja. Eles são os que não precisam necessariamente ser calculados, pois ou são os dois primeiros, ou são os que podem ser espelhados, visto que os números equidistantes dos extremos são iguais. Como podemos observar na tabela, lendo da esquerda para a direita ou da direita para a esquerda, os coeficientes são os mesmos. Vale lembrar que se n fosse par o número de coeficientes seria ímpar e por isto o termo central precisaria ser calculado, já que o mesmo não seria espelhado por ser o coeficiente central.
Na prática não precisamos montar a tabela, basta realizarmos os cálculos passo a passo para obtermos os coeficientes binomiais. Utilizamos o recurso da criação de uma tabela apenas para estruturar melhor as explicações.
Agora podemos continuar o desenvolvimento de (2x + 3)7 do ponto em que paramos:
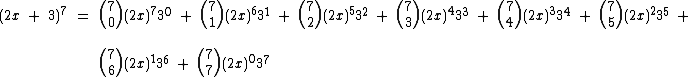
Substituindo os números binomiais e resolvendo as potências temos:
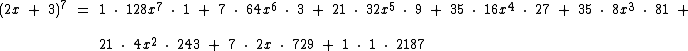
Concluindo as multiplicações chegamos ao resultado desejado de (2x + 3)7: